Вы не зашли.
 #1.
TLENS
Off
#1.
TLENS
Off
(14)
Moderator
2011.06.05 00:12
У нас пацанчик решил по понтоватся и задал нам задачку надо нарисовать такую фигуру не отрывая руки боле 2 раз и не проводя по одной и той самой линии.
Я чет нефига не могу. Он шампанское обещал. Вот мне интерестно возможно ли это?
Отредактировано TLENS (2011.06.05 05:05)
 #2.
Nu3oN
Off
#2.
Nu3oN
Off
(11)
Moderator
2011.06.05 05:05
х.м! а реально? тут как минимум эллипс надо использовать и кисть!

Я буду лучше голоден, но между креслом и рулем и на дороге.
 #3.
tipsun
Off
#3.
tipsun
Off
(19)
Moderator
2011.06.05 06:06
Вот еще подкину

В принципе, очень известные...
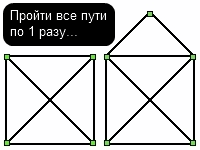
.:
Google::Теории графов:.
> Графами были названы схемы, состоящие из точек (вершины графа) и соединяющих эти точки отрезков прямых или кривых (ребра графа). Одна из разновидностей на рис. выше.
> Степень вершины - количество ребер графа, исходящих из этой вершины.
> Вершина называется нечетной - если степень этой вершины нечетная, четной - если степень этой вершины четная.
Закономерности:
- Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине. Фигура (граф), которую можно начертить не отрывая карандаш от бумаги, называется
уникурсальной.
- Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
- Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
.:Перерисовал, для наглядности:.
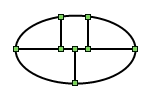
Вложения
Задачки.png
4kb
{200x150}
[
загрузок: 2914]
Re.png
2kb
{150x100}
[
загрузок: 2353]
Отредактировано tipsun (2011.06.05 07:07)
 #4.
TLENS
Off
#4.
TLENS
Off
(14)
Moderator
2011.06.05 07:07
tipsunНу это понял но в задаче разрешается за три раза
Отредактировано TLENS (2011.06.05 07:07)
 #5.
tipsun
Off
#5.
tipsun
Off
(19)
Moderator
2011.06.05 13:01
http://acadclasses.narod.ru/math/lecture5.htm - см. утверждение 1 и 2

- - - -
Как я понял:
У данного графа 8 вершин.
2n=8 (Вершин) <=> n=4 (Пар)
Можно нарисовать лишь при n-1 <=> 4-1=3 "отрывании ручки от пути".
- - - -
Но у меня не получилось.
Только при 4 отрываниях получается.
Для 4 вершин все сходится... Ну квадрат с диагоналями.
Отредактировано tipsun (2011.06.05 14:02)
 #6.
TLENS
Off
#6.
TLENS
Off
(14)
Moderator
2011.06.05 19:07
tipsunА я за три отрывания нарисовал
 #7.
tipsun
Off
#7.
tipsun
Off
(19)
Moderator
2011.06.05 19:07
Покажи, ну рисунок в пейнте. 1 отрывание... 2 отрывание...

Отредактировано tipsun (2011.06.05 19:07)
 #8.
TLENS
Off
#8.
TLENS
Off
(14)
Moderator
2011.06.06 16:04
Я говорю что за три отрывания а не раза, это получается 4 раза.
Отредактировано TLENS (2011.06.06 17:05)
 #9.
TLENS
Off
#9.
TLENS
Off
(14)
Moderator
2011.06.06 17:05
Ну вот смотри я просто последнее отрывания не считаю
TLENS написал:
Ну вот смотри я просто последнее отрывания не считаю
а, я последнее считал. Вот почему не сходилось





